SpaTools: ShrinkWrap - A tool to create Concave Polygon

 

Relationships in all environments have boundaries which are generally acceptable limits usually set for permissible behavior to a specific relation. The flexibility of a boundary varies with the relationship…formal relationships have a very rigid boundary and cordial relationships (family and friends) cling-on very softly.

TIN (Triangulated Irregular Network) is a relationship known in the GIS or CAD environment developed from survey data points. Workflows in these environments take an optional input of “Boundary” to limit outputs for the extents of a surface. AutoCAD Civil 3D, BricsCAD or any other CAD package is used in the CAD environment whereas ArcGIS 3d Analyst, QGIS or any other GIS software are tools in the GIS environment. The surface generated from TIN is then utilized to create contours, volumetric computations (Cut/Fill) and other processes.

The “Boundary” refines such processes for a surface in the TIN. It is created by connecting exterior data points forming a polygon. I started to write blogs on AutoCAD with a prefix of SpaToolsto introduce a set of tools. The first blog of this series was based on a condition that: 

"Every point in the input point set is vertex of resulting polygon".

(See the first SpaTool to “Construct polygon / Polylines from a set of points”).


This SpaTool works well when extents of boundary properties, houses or lakes etc are required to be constructed from survey data points. The algorithm is unique and based on an idea from the Land Record System of Sindh, Pakistan. (Up-coming Blog).

However, the formal (default) setup for a “Boundary” is always a “Convex Hull”. The “Convex Hull”is a polygon with the shortest perimeter to enclose a set of points, such that:

  • All the interior angles are less than 180 resulting all the vertices points outwards, away from the center.
  • A line drawn through a convex polygon will intersect the polygon exactly twice.
  • The diagonals of a convex polygon lie entirely inside the polygon.

Various algorithms are proposed for constructing the “Convex Hull”of a finite set of points with varying complexities and can be found under the subject of “Computational Geometry”. I have implemented the well-known“Grahm Scan Convex Hull” algorithm.(See the SpaTool to "Construct Convex Hull from set of Points").

This blog aims at describing the informal flexibility which can “ShrinkWrap” the “Convex Hull” cordially to the spread of a point data set in the TIN. But first, let us have a recap of the properties of a non-convex, i.e. a concave polygon:

  • A polygon that has one or more interior angles greater than 180° resulting some vertices point 'inwards', towards the center.  
  • It looks sort of like a vertex has been 'pushed in' towards the inside of the polygon.
  • A line drawn through a concave polygon can intersect the polygon in more than two places.
  • Some of the diagonals of a concave polygon will lie outside the polygon.
  • Regular Polygons are never concave by definition.

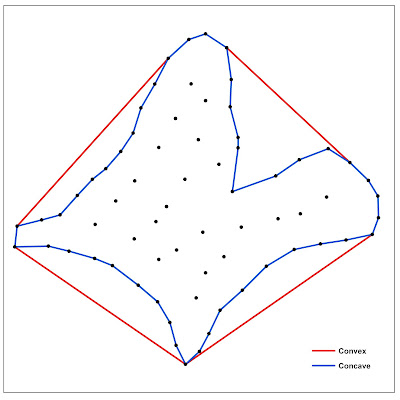
The difference between Convex and Concave polygon around a cluster of points is illustrated below:



It might be noted that, we will always have  ONE solution / output of a convex polygon for the same set of points regardless of the type of algorithm used.

But, for the same set of points we may have different outputs of concave polygons as illustrated below:


From the illustrations above, it can be seen that convex edges of the convex hull can be concaved towards the center of the “Convex Hull” polygon to produce a concave polygon.

But what is the limit for this concavity? … This is my point of interest.

Leaving aside this “Concavity Index” for the time being, let’s focus on the conditions to be satisfied.After all the algorithm must converge in a finite time with a valid solution;

  •  The resulting polygon must have vertices from the input set of points.

  • All the other points must lie inside the resulting polygon.

  • The polygon should NOT be self intersecting.

If “Convex Hull” is a polygon with Zero Concavity Index (CI = 0), then we can say that a concave polygon will have greater than Zero Concave Index (CI) … the most concave polygon will be with the highest concavity index, i.e.Unity (One).

Based on these conditions and assumptions, I formulated an algorithm and implemented it using the AutoCAD .Net API. It is now included as part of the SpaTools.

It takes two inputs:

  • Finite set of 2D  points (AutoCAD point objects).
  • A concavity index (From Zero to One)

The Zero CI (Concavity Index) will alwaysresult in a “Convex Hull”. While a CI of Unity (One) will construct the most concave polygon introducing noses and ears. The points can be selected on screen and the CI value can be chosen by moving a slider towards left or right as depicted below:


Here is a demo of the latest SpaTool when applied on a point data set with different CI values.


Polygon with Zero CI resulting in a Convex Polygon



Polygon with 0.5 CI resulting in a Concave Polygon


Polygon with 0.75 CI resulting in a Concave Polygon

Polygon with 0.8 CI resulting in a Concave Polygon

"LINEWORKSHRINKWRAP" is an existing command in AutoCAD Civil 3D which runs only on the lines, polylines and other linear objects. However, to create a confined boundary around points, I couldn’t find anything in AutoCAD or BricsCAD … :)

This addition to SpaTool was certainly useful for me when a confined boundary around the points was required for surface modeling.

Download the new SpaTool and use it on different sets of points with different Concavity Index values. Your feedback and comments are always welcome.

The updated SpaTools DLL can be downloaded from Cadomation.

Comments

Post a Comment

Popular posts from this blog

SpaTools: Import Lidar Point Cloud (LAS/LAZ) files into AutoCAD

Image
Point clouds are large data sets composed of 3D point data. These geographic point data is collected mostly by Laser scanners and drones equipped with LIDAR (Light Detection And Ranging) sensors. In addition to these directly collected LIDAR point cloud data, the aerial RGB images collected by drones are processed using Image Processing & Computer Vision Algorithm based software such as Pix4D, Agisoft Photoscan or DroneDeploy to produce RGB Point Clouds in LAS file format. Besides that, the well known image processing software such as ERDAS Imagine Leica Photogrammetry Suite (LPS), ENVI and PCI Geomatica produce output in LAS file format when stereo/tri-stereo satellite images (WorldView-2, WorldView-3, SOPT 5/6/7 & Pleiades) are processed.     LAS is an industry standard file format defined by the American Society of Photogrammetry and Remote Sensing (ASPRS) that includes a system of point classification. A processed LAS file may have points classified as bar...
Read more

How to Clip objects in AutoCAD

Image
There is a tool named as CLIP in ArcGIS which cut out a piece of one feature class using one or more of the features in another feature class as a cookie cutter. This is particularly useful for creating a new feature class as study area or area of interest (AOI) that contains a geographic subset of the features in another, larger feature class. It is often needed to CLIP all the objects contained completely inside a polygon to a new drawing. The type of the objects may vary from simple objects like polylines, lines, circles, text to complex objects like splines, arcs, hatches, blocks etc. Since the release of AutoCAD 2008, a new command EXPORTLAYOUT was introduced to export all the objects in all the viewports of the layout to a separate drawing. I am writing this article because most of the CAD users are not aware about the power of this magical command of Autocad and use TRIM command to trim all the objects one by one which are outside of the desired polygon. It is h...
Read more

Creating Contour Maps in ArcGIS and Conversion to AutoCAD drawing

Image
A topographic map is simply the two dimensional representation of a portion of three dimensional surface of earth. Topographic maps provide the detailed information about the natural and man-made aspects of the terrain, but are best known for their series of contour lines that show elevation changes, and colors signifying varying land types and bodies of water. Contour lines are used to determine elevations and are lines on a map that are produced from connecting points of equal elevation (elevation refers to height in feet, or meters, above sea level). By reading contour lines, one can measure the steepness of a hill, the height of a mountain, and even the depth of a lake or ocean . These lines are evenly spaced apart. This spacing is called the contour interval. For example, if your map uses a 10-foot contour interval, you will see contour lines for every 10 feet (3 meters) of elevation -- lines at 0, 10, 20, 30, 40, and so on. Different maps use different intervals, dependin...
Read more

SpaTools: Extract Topographic Profile From Contours In AutoCAD

Image
A topographic map is simply the two dimensional representation of a portion of three dimensional surface of earth. Topographic maps provide the detailed information about the natural and man-made aspects of the terrain, but are best known for their series of contour lines that show elevation changes, and colors signifying varying land types and bodies of water. Contour lines are used to determine elevations and are lines on a map that are produced from connecting points of equal elevation (elevation refers to height in feet, or meters, above sea level). By reading contour lines, one can measure the steepness of a hill, the height of a mountain, and even the depth of a lake or Ocean . The contours can be generated by a DEM (Digital Elevation Model), TIN (Triangular Irregular Network) or a surface using different software such as ArcGIS.  Read the blog about How to generate contours from DEM and create a topographic map in Autocad. Most of the topographic maps used for p...
Read more

Gunter Chain / Surveyor's Chain

Image
“ What is the length of cricket pitch?”  “It is equal to 22 yards”. Cricket  is a bat-and-ball game played between two teams of eleven players on a field at the center of which is a 22 yard pitch with a wicket at each end, each comprising two bails balanced on three stumps.  Recalling the memories of childhood, we use to place the wickets by pacing out a distance of 22 paces by walking. At that time, we were not aware neither interested to know the exact length of cricket pitch. But this time, the question raised in my mind that why it is 22 yards!! ?? Why it is not like 22 meters or 25 yards or 20 yards? Cricket Pitch The standard length of cricket pitch is simply one Gunter chain (Surveyor’s chain) since the first known code of Laws in 1744 and it is believed this length had been in use since the introduction of Gunter's chain  in 1620 . Throughout recorded history surveyors have used ...
Read more

SpaTools: Toolbar with all tools

Image
Since January 2020, I started writing blogs about the custom tools developed for AutoCAD. All those blogs are entitled with the prefix of “SpaTools” . Currently, ten (10) different tools have been added to SpaTools.DLL . For each tool, I have published a blog with the explanation of its usability and some basic information. The readers not only appreciated it but also suggested to improve and extend it further by adding more tools such as Export CSV, KML, LAS, GPX, SHP etc and other cartographic tools. Besides that, it was suggested by some users to develop it as a Toolbar . In the response of that suggestion, I have developed it as a toolbar. The DLL file can be downloaded from the link  at the bottom of this page. Prior to loading in AutoCAD, unblock it. Right Click on the DLL file and check the unblock checkbox and apply. Load the DLL into AutoCAD using NETLOAD command.    The commands are categorized into three panels:  Import , Create Features an...
Read more